Big picture of nomograph construction

Nomographs of PyNomo are constructed by writing a python script that defines the nomograph parameters and initializes class Nomographer(parameters) to build the nomograph.

Nomograph is constructed by defining axes that are used to build blocks. If there are more than one block, they are aligned with each other in order to construct the nomograph.

A simple example of pseudocode of typical PyNomo structure is the following:

from pynomo.nomographer import *  # this loads the needed pynomo class
# define block 1
axis_params_1_for_block_1 = {...}
axis_params_2_for_block_1 = {...}
axis_params_3_for_block_1 = {...}
block_1 = {...}

# define block 2
axis_params_1_for_block_2 = {...}
axis_params_2_for_block_2 = {...}
axis_params_3_for_block_2 = {...}
block_2 = {...}

# define nomograph
main_params = { 'filename': 'filename_of_nomograph.pdf',  # filename of output
                'block_params': [block_1,block_2],        # the blocks make the nomograph
                'transformations':[('scale paper',)],     # these make (projective) transformations for the canves
                }
# create nomograph
Nomographer(main_params)

It is to be noted that nomograph is defined as python dictionaries that constitute one main dictionary that is passed to Nomographer class.

Axes

A nomograph consist in simple terms of axes (or scales) that are positioned in a way to fulfil the equation to be graphed. Axes (or grids or graphs) are the leafs that build the tree of a nomograph. Defining axes and their appearance is major work in nomograph construction. Different possibilities are illustrated in Axes chapter.

Blocks

Blocks relate axes to each other. Each block fulfils some equation where axes are the variables. The following blocks below with corresponding equations are the core of PyNomo. These are used as easy building blocks for nomograph construction. If these do not suffice one can build as complex nomograph as one wishes by using determinants in type 9.

Type 1

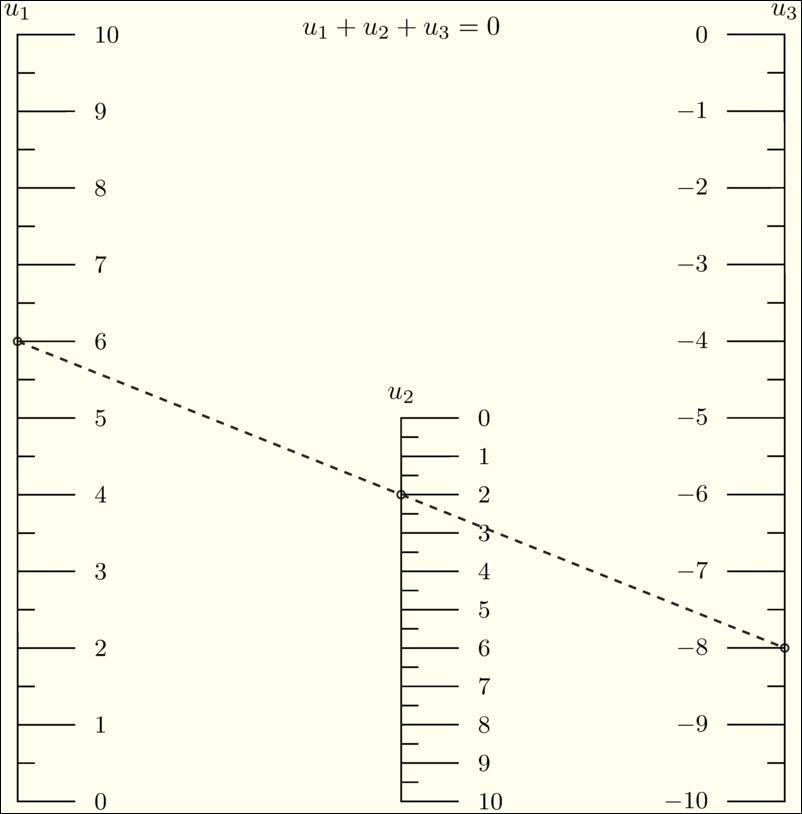
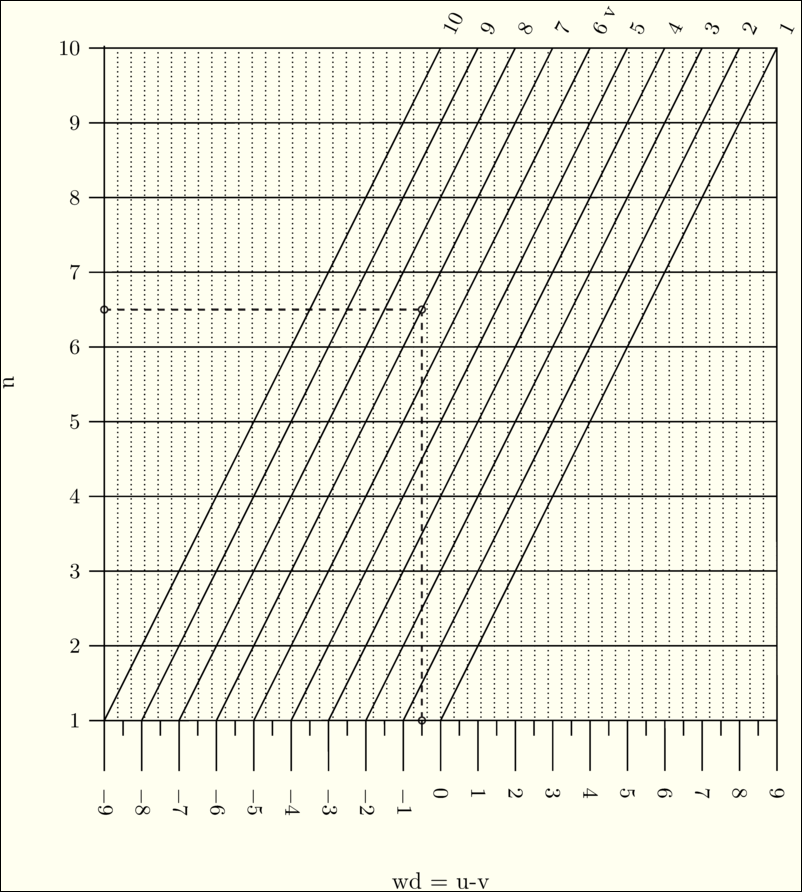
\(F_1(u_1)+F_2(u_2)+F_3(u_3)=0 \,\)

type1image

Type 2

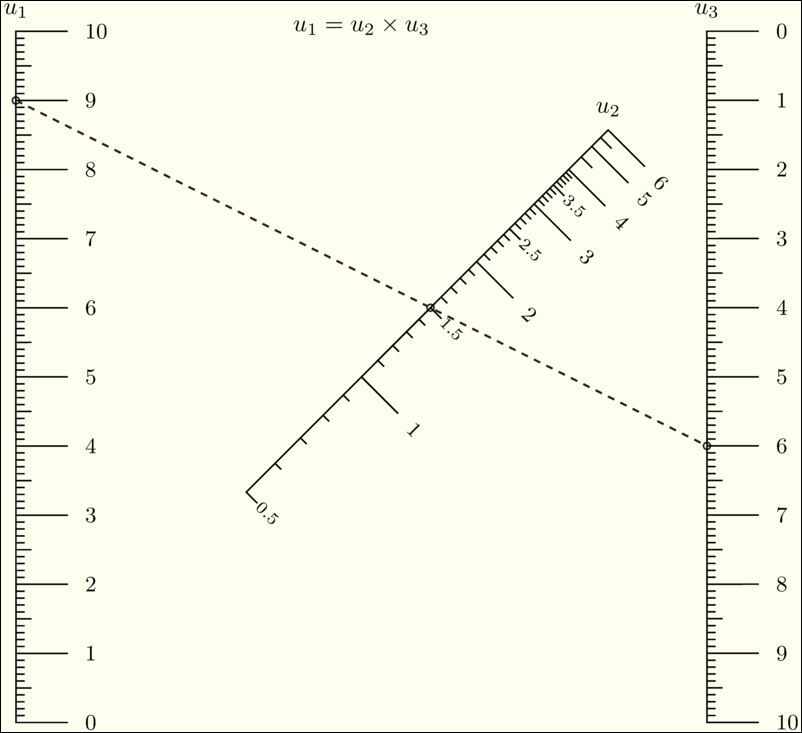
\(F_1(u_1)=F_2(u_2) F_3(u_3) \,\)

type2image

Type 3

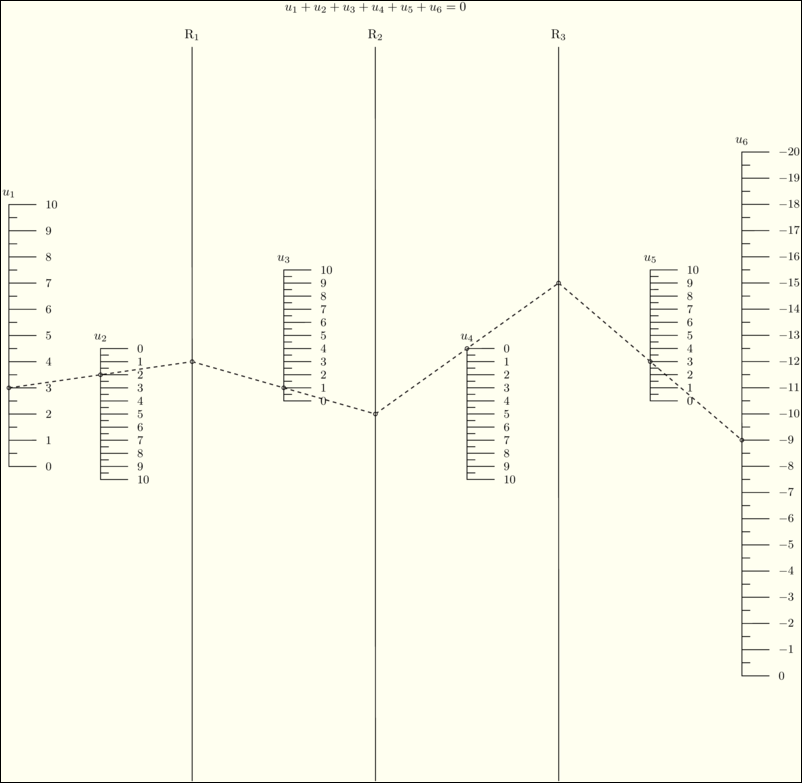
\(F_1(u_1)+F_2(u_2)+\cdots+F_N(u_N)=0\)

type3image

Type 4

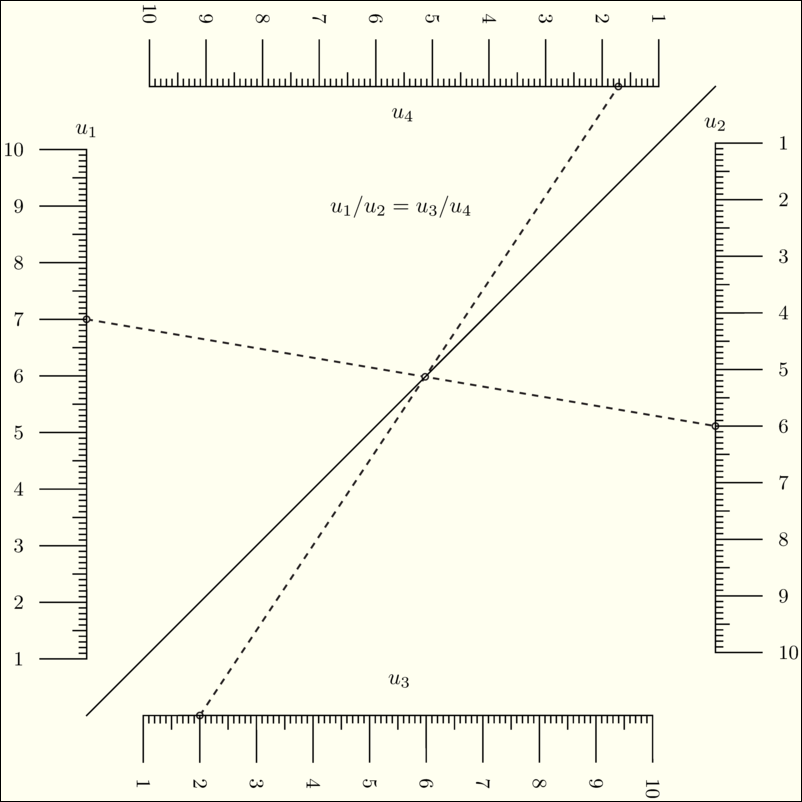
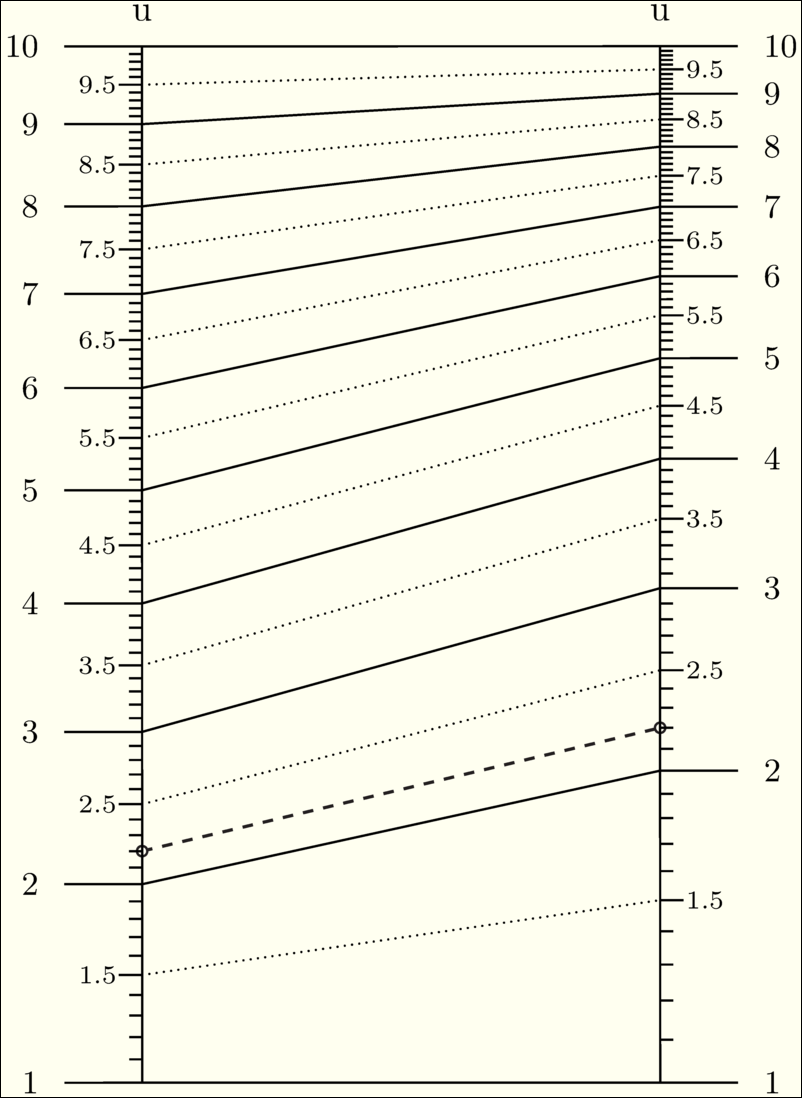
\(\frac{F_1(u_1)}{F_2(u_2)}=\frac{F_3(u_3)}{F_4(u_4)}\)

type4image

Type 5

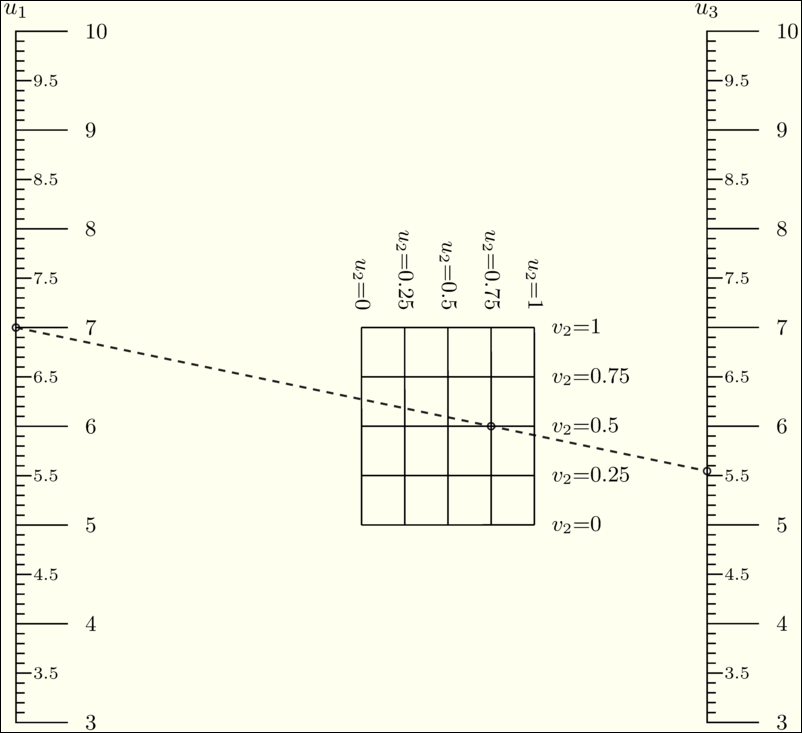
\(F_1(v) = F_2(x,u). \,\)

type5image

Type 6

\(u=u \,\)

type6image

Type 7

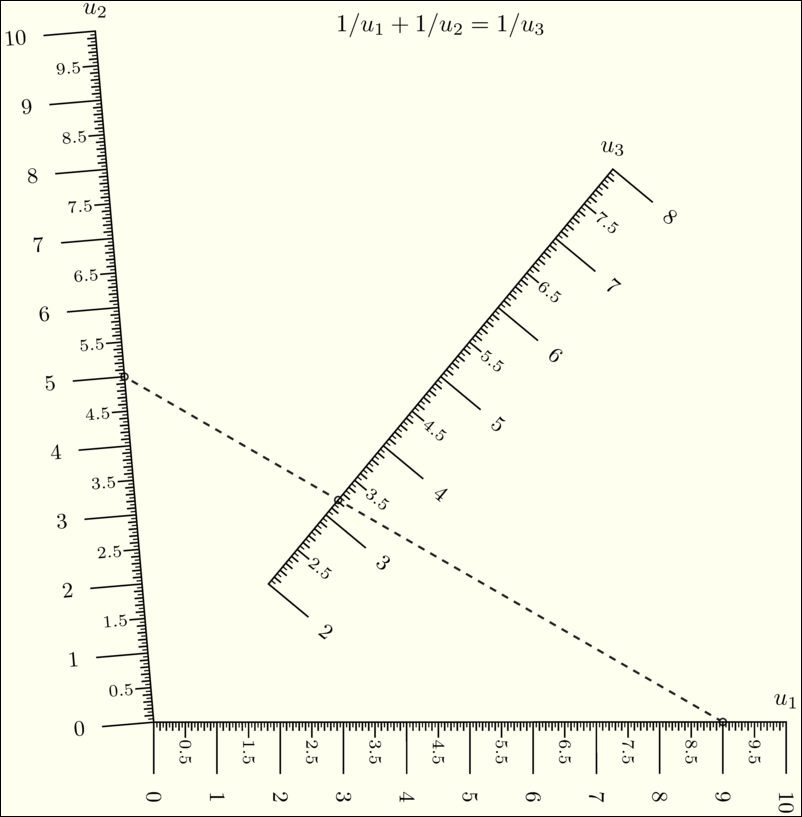
\(\frac{1}{F_1(u_1)}+\frac{1}{F_2(u_2)}=\frac{1}{F_3(u_3)} \,\)

type7image

Type 8

\(y = {F(u)} \,\)

type8image

Type 9

\(\begin{vmatrix}F_1(u_1[,v_1])& G_1(u_1[,v_1]) & H_1(u_1[,v_1])\\ F_2(u_2[,v_2])& G_2(u_2[,v_2]) & H_2(u_2[,v_2]) \\ F_3(u_3[,v_3])& G_3(u_3[,v_3]) & H_3(u_3[,v_3]) \end{vmatrix} = 0\)

type9image

Type 10

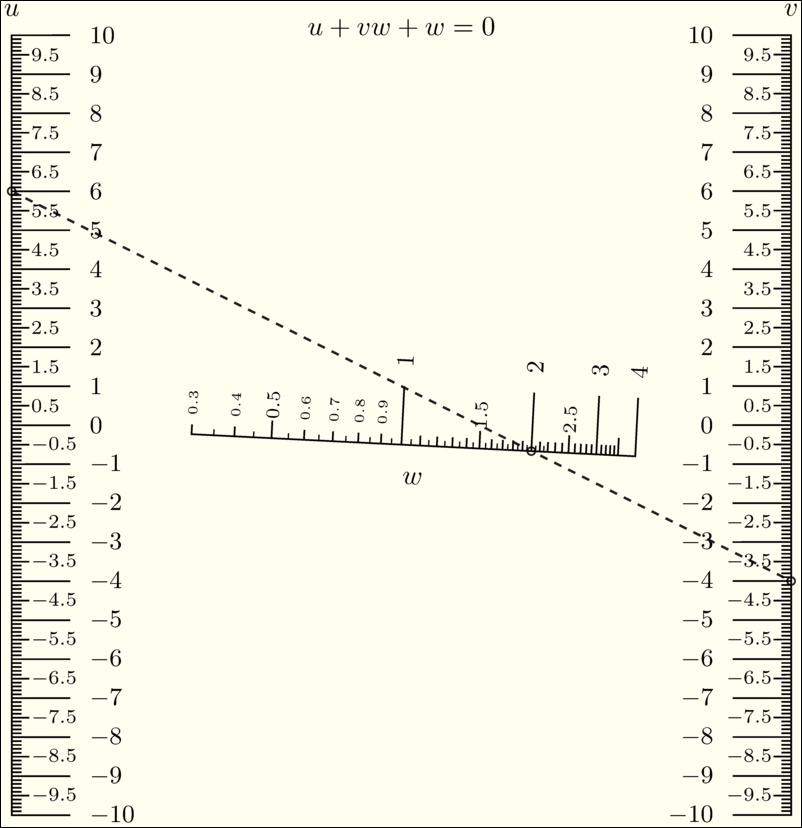
\(F_1(u)+F_2(v)F_3(w)+F_4(w)=0 \,\)

type10image

Combination of blocks

If a nomograph consists of many equations that are aligned, a compound nomograph is constructed. Chapter compound nomograph discusses block aligment in detail.

Transformations

Scales shall be transformed in order to use given space (paper) optimally. Chapter Transformations discusses transformations.